AEROZOLOTERAPIA
Felix, qui potuit rerum cognoscere causas.
Dawka emitowana
Czy wyróżnienie dawki emitowanej jest konieczne, skoro pochodzi ona bezpośrednio z dawki nominalnej, a jeśli tak, to dlaczego?
Życie codzienne uczy nas, że praktycznie nie ma zdarzeń idealnych, w których zawsze i bezwarunkowo, w każdej sytuacji konkretne działanie da przewidywalny i w 100% powtarzalny efekt. Założenie, że zawsze i bezwzględnie 100% dawki nominalnej ulegnie przekształceniu w dawkę wyemitowaną jest założeniem błędnym. W przypadku każdego rodzaju inhalacji o skali strat decyduje specyfika konstrukcji poszczególnych urządzeń technicznych, a zwłaszcza najprostszych nebulizatorów.
Dokonajmy przeglądu kilku typowych sposobów tworzenia aerozolu i zastanówmy się, które z nich generują najwyższe starty dawki oraz, co jest niezwykłe istotne, które z nich pozwalają na obiektywne oszacowanie tych strat.
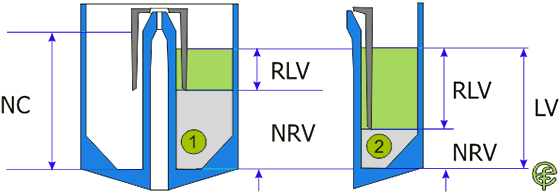
Wiadomo, że dawka nominalna w nebulizacji podlega pewnym ograniczeniom związanym z pojemnością nebulizatora NC. Na rycinie uwzględniono kolejną istotną cechę konstrukcyjną : objętość rezydualną nebulizatora (NRV).
Ryc. 1. Związek między pojemnością nebulizatora NC, objętością rezydualną nebulizatora NRC,
globalną objętością płynu LV oraz możliwą do wykorzystania, realną objętością płynu RLV
Objętość rezydualna nebulizatora może być rozumiana jako „pułapka na dawkę” lub „czarna dziura pochłaniająca dawkę” : dawka nominalna, która „wpadła w pułapkę” lub „wpadła w czarną dziurę” nigdy się z niej nie wydostanie. Zrozumiała jest zatem konieczność rozróżnienia dawki nominalnej i dawki emitowanej – wyemitować można jedynie tę część dawki nominalnej, która nie znajduje się w obrębie pułapki NRV. Z rozważań na temat dawki nominalnej wiadomo, że jej nośnikiem jest albo „fabryczny” roztwór leku o stężeniu DPC, albo mieszanina roztworu leku i rozcieńczalnika o stężeniu DPC. Na rycinie 1 zauważamy, że:
- objętość płynu LV nie może przekroczyć wartości NC (pojemności nebulizatora)
- objętość płynu LV dzieli się na część bezpowrotnie uwięzioną w NRV, niemożliwą do wyemitowania
- objętość płynu LV dzieli się na część „powyżej pułapki”, realną objętość płynu RLV, możliwą do wyemitowania
- istnieje odwrotna zależność miedzy NRV a RLV : w sytuacji 1 duża wartość NRV wymusza zubożenie RLV, w sytuacji 2 niskiej NRV towarzyszy wysoka wartość RLV
Ryc. 2. Sposób wyliczenia dawki emitowanej z wykorzystaniem parametrów: DPC (lub DSC), LV, NRV i RLV
Nie bez przyczyny nebulizacja nie tylko pretenduje, ale jest w rzeczywistości metodą najbardziej precyzyjną w odniesieniu do wziewnego dawkowania leków. Jak na innych etapach planowania zabiegu, tak i w tym przypadku dawkę emitowana można dokładnie wskazać. Dokonajmy analizy treści ryc. 2. Rozumiejąc, że dawka nominalna zawarta jest w objętości płynu LV, określamy przede wszystkim objętość płynu RLV, którą można realnie wyemitować (RLV = LV – NRC). Znając stężenie oryginalnego roztworu leku DPC lub stężenie leku w zmodyfikowanej mieszaninie DSC wyliczamy dawkę emitowaną jako iloczyn DPC x RLV lub analogicznie DSC x RLV.
Umiejętność radzenia sobie z problemem leku „znikającego” w przestrzeni martwej nebulizatora jest łatwa do przyswojenia. W zdecydowanej większości sytuacji regułą jest bowiem wstępne uzupełnienie („zalanie”) przestrzeni NRV lekiem a następnie dodanie kolejnej, niezbędnej do uzyskania efektu terapeutycznego, objętości leku.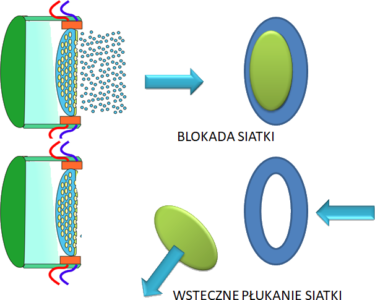
Niestety, w przypadku zawiesin reguły gry ulegają zmianie: o ile medium nadal bez przeszkód przenika przez otwory membrany, o tyle kryształy zawiesiny mogą zatykać otwory siatki – lek nie przedostaje się do chmury aerozolu.
Kolejnym nieporozumieniem jest utożsamianie zabiegu skutecznego odblokowania siatki z możliwością efektywnego podania leku. To prawda, że odblokowana siatka umożliwi kontynuację tworzenia aerozolu, jednakże jego skład będzie różny od oczekiwanego: będzie miał skład z przewagą drobin pozbawionego leku medium oraz nielicznych kryształów leku, których rozmiary były na tyle małe, że pokonały „wąskie gardło” otworów membrany.
Wszystkie kryształy większe od średnic otworów siatki nigdy nie opuszczą wnętrza inhalatora siateczkowego.
Niestety, skali tego zjawiska nie ujawniają ani producenci leków ww formie zawiesin (brak danych o stopniu rozdrobnienia i zróżnicowania fazy stałej zawiesiny), ani producenci sprzętu *).
*) W gronie producentów wyróżnia się rodzima, polska firma, której badania nad emisją aerozolu z inhalatorów siateczkowych dają rzetelne podstawy do dawkowania leków w oparciu o udokumentowany materiał źródłowy. W odniesieniu do dawki emitowanej dla budezonidów współczynnik „przepuszczalności” membrany wynosi od 80% – 95%.
Nebulizatory ultradźwiękowe cechuje bardzo niska objętość martwa, o ile mamy na myśli wyłącznie obszar tworzenia aerozolu. Jeśli jednak prześledzimy inne cechy konstrukcyjne urządzenia, a w szczególności drogę aerozolu od miejsca jego tworzenia do miejsca jego poboru okazuje się, że istnieją uzasadnione obawy co do ukrytych strat dawki.
Sytuację komplikuje dodatkowo kwestia właściwej klasyfikacji zjawisk, co rodzi pytanie o dopuszczalność wskazania np. zjawisk inercyjnych czy sedymentacji cząstek w systemie rur przewodzących aerozol jako elementu pojęcia przestrzeni martwej. Pomijając te wątpliwości można przyjąć, że w odniesieniu do nebulizatorów ultradźwiękowych :
° dysponujemy udokumentowaną wiedzą o niskiej wartości przestrzeni martwej per se
° nie dysponujemy danymi na temat skali ubytku dawki w systemie rur doprowadzających
Ideę rozszerzenia pojęcia przestrzeni martwej omówiono poniżej.
W przypadku dozowników pMDI stosowanych (błędnie!) bez komory inhalacyjnej sytuacja jest jasna: dyskusja na temat przestrzeni martwej jest nieuzasadniona: wyzwalana jest deklarowana dawka leku, a ewentualny błąd jest znikomy.
Dozowników pMDI nie można jednak postrzegać przez pryzmat korzystnego braku przestrzeni martwej pamiętając, że kluczowym mankamentem metody są istotne straty dawki w mechanizmie inercyjnym, omawianym w odrębnym artykule.
Poprawne stosowanie dozownika pMDI z komorą inhalacyjną, pomimo korzystania z tego samego inhalatora, tworzy dla dawkowania leku kontekst zdecydowanie odmienny. Kluczem do uzmysłowienia sobie tej różnicy jest analiza zdarzeń nie w punkcie tworzenia, lecz w punkcie poboru aerozolu, czyli na wyjściu ustnika komory inhalacyjnej. O ile w przypadku pMDI dysponowaliśmy wiedzą o fakcie pojawienia się aerozolu w dawce emitowanej a obszar wątpliwości wiązał się z pytaniami o nieznaną objętość czy prędkość strumienia aerozolu, o tyle w przypadku komory inhalacyjnej znamy praktycznie jedynie jej objętość i fakt, że do chwili wykonania wdechu przez chorego aerozol nie jest spontanicznie emitowany z komory.
Nie wiadomo praktycznie nic na temat skali strat inercyjnych cząstek leku na ścianach komory inhalacyjnej, nie znamy tempa ich sedymentacji, nie znamy wreszcie stopnia zmiany proporcji między liczbą cząstek frakcji CPF/FPF.
Reasumując – mamy racjonalne przesłanki do przypuszczenia, że część dawki wyzwolonej z inhalatora zostaje uwięziona w obrębie komory inhalacyjnej, niestety nie znamy skali tego zjawiska co oznacza, że nie mamy wiedzy na temat dawki, którą leczymy.
Co do zasady, poprawnie wykorzystanie techniki DPI zwalnia z obowiązku rozważań nad kwestią przestrzeni martwej, czy szerzej – różnic między dawką nominalna a dawką emitowaną. Z drugiej strony, dozowniki suchego proszku cechują różnice konstrukcyjne, odmienność preparatyki substancji czynnych i nośnikowych, poprawności doboru do możliwości wdechowych konkretnego pacjenta itd.
Można jedynie spekulować nad konsekwencjami nieefektywnej inhalacji, których konsekwencją byłoby „uwięzienie” części leku w dozowniku, co stanowi analogię do pojęcia przestrzeni martwej:
° niepełne opróżnienie kapsułki lub blistra
° niepełne rozdzielenie cząstek leku właściwego od cząstek substancji nośnikowych.
